OpenATPOL

[Download] [Project page] [Online map] [Tutorial (Polish)]

Swietnie opracowany po polsku opis siatki dla nie-programistow mozna odnalezc na stronie Instytutu Botaniki PAN. Znajdziemy tam tez opis siatki PolBiG.

About

This project is a reference, well-tested implementation of conversion algorithms for Polish geobotanical grids ATPOL and PolBiG.

The ATPOL grid was developed in Institute of Botany, Jagiellonian University, Krakow, Poland for the immortal 1970s work called Distribution atlas of vascular plants in Poland. It covers 700 x 700 km area (with whole Poland inside).

The grid was initially drawn by hand on available maps, then copied also by hand, as no tools like xero were then available. When GPS tools became popular, Institute of Botany published its online version with computed coordinates (with 1 second accuracy).

These coordinates were used by researchers as a reference, however the mathematical background of this grid was never published. In Polish internet fora, there was a long discussion without any definite conclusion. The only one possible conversion was to take the tabularized grid data and to perform the linear (incorrect, but the only one possible) interpolation.

The extensive mathematical research done in 2015 uncovered the mathematical mystery of the ATPOL grid. The exact solution was found by reverse engineering of the tabularized values and fitting dozens of geographical projections. The findings and proposed algorithm was published (in Polish) in:

L. Komsta. ATPOL geobotanical grid revisited – a proposal of coordinate conversion algorithms. Annales UMCS Sectio E Agricultura 2016, 71, 1, 33-37.

As one of the reviewers of above paper explicitly asked for consulting these results with Institute of Botany before publication, the author was forced to try and got the confirmation in private correspondence, that this reasoning is correct. The further numerical investigation was then published in

M. Verey. Theoretical analysis and practical consequences of adopting a model ATPOL grid as a conical projection defining the conversion of plane coordinates to the WGS 84 ellipsoid. Fragm. Flor. et Geobot. Pol. 2017, 24, 2, 469-488.

Finally, on 16th October 2017, the creators of ATPOL grid confirmed officially the reasoning described in these two papers, confirming also the use of WGS84 coordinate system.

The next step after the confirmation was to think and propose the unified way to denote the grid squares for non-decimal (other than 100, 10, 1 km etc.) resolution, which appeared some time later:

M. Verey, Ł. Komsta: Standardization of the notation dividing the ATPOL grid (Standaryzacja zapisu podziałów siatki ATPOL). Fragm. Flor. et Geobot. Pol. 2018 25(1): 107-111.

The PolBiG grid is a new binary approach for geobotanical research, proposed recently in:

M. Verey. Polish Binary Grid – PolBiG (Polska Siatka Binarna - PolBiG). Fragm. Flor. et Geobot. Pol. 2018 25(2): 255-272.

Implementation of PolBiG is also under inclusion to OpenATPOL project.

Definition

The ATPOL projection is simple conic centrographic projection with one tangent (the cone touches the sphere but does not cross it) at the latitude \(\varphi_0 = 52^\circ\)N. The central (vertical) meridian is chosen to be \(\lambda_0 = 19^\circ\)E. The central point of the projection \((52^\circ N, 19^\circ E)\) is defined to have coordinates \(x_0 = 330\)km, \(y_0 = 350\)km. The Earth radius is chosen to be \(R = 6390\)km. The coordinates increase towards South and East (they are equal to zero in NW corner of the grid). It is quite similar to Equidistant Conic Projection (EQDC), but the latter is orthographic (the projection rays goes in ATPOL from the Earth center, whereas in EQDC they are orthogonal and parallel).

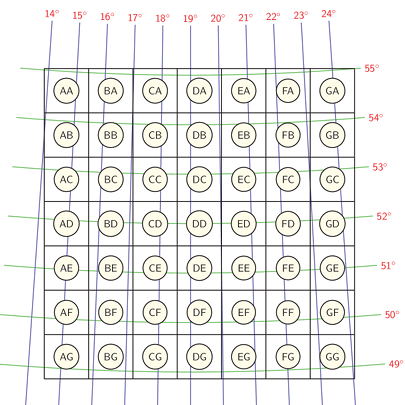
The first two letters denote the square with 100 km size, as in the figure above. The smaller 10 x 10km square units are denoted by two additional numbers, but in reverse way (\(y\) is the first coordinate). The division can be done recursively, so AB1234 is a square with 1 km dimension, AB987654 is 100m, and so on.

The atypical resolutions can be archieved by precede the last division by a small letter d (binary division), c (quaternary division), or p (quinary division).

The \(x,y\) coordinates are never used in practice, however they represent an exact position in ATPOL projection and they are an intermediate step when geographical coordinates are converted to ATPOL grid.

When a grid is given, the position inside the square can be done in relative way by giving \(o_x\) and \(o_y\) values in range \((0,1)\). Two zeros means upper left (NW) corner of the square, whereas two 0.5 values means the middle of the square.

The coordinates are in currently used WGS84 coordinate system. Although the old maps could be drawn in Pulkowo 1942 coordinate systems, the difference between these coordinate systems is less than hand-copying error of the maps that time.

Although the projection seems to be quite strange (as there were no printed maps in such projection, moreover the assumed Earth radius is equal to 6390 km), this projection was chosen as a compromise by the ATPOL authors to fit all available hand-drawn maps. Therefore, these algorithms can be surely used without any risk that they are incorrect.

Example

For example, the coordinates of the Palace of Culture and Science in Warsaw can be represented as:

  1. As “lonlat” pair, \(\varphi = 21.006062^\circ\)N, \(\lambda = 52.231727^\circ\)E.
  2. As “xy” pair, \(x = 467.0110005\)km, \(y = 322.2659527\)km.
  3. As a point in the following ATPOL squares, with corresponding relative offsets inside:
Meters Grid \(O_x\) \(O_y\)
100000 ED 0.67011001 0.22265953
50000 EDd01 0.34022002 0.44531906
25000 EDc02 0.68044004 0.89063812
20000 EDp13 0.35055005 0.11329765
10000 ED26 0.70110010 0.22659530
5000 ED26d01 0.40220020 0.45319060
2500 ED26c02 0.80440040 0.90638120
2000 ED26p13 0.50550050 0.13297650
1000 ED2627 0.01100100 0.26595300
500 ED2627d00 0.02200200 0.53190600
200 ED2627p10 0.05500500 0.32976500
100 ED262720 0.11001000 0.65953000
50 ED262720d10 0.22002000 0.31906000
20 ED262720p30 0.55005000 0.29765000
10 ED26272061 0.10010000 0.59530000

One should remember about the GPS accuracy, so the last example has any sense only with geodesic GPS receivers.

The \(o_x\) and \(o_y\) values are never given in publications, they are only needed to store exact position and give the ability to perform the reverse computations.

ATPOL in GIS software

The ATPOL projection is centrographic and thus it is not equidistant, equal-area nor conformal. Therefore, it has not been implemented for a long time due to almost no interest.

In November 2017, the code of such a projection was submitted as a pull request to PROJ4 repository. Since version 5.0.0 of PROJ4, the ATPOL projection can be used as Central Conic projection, implemented as “ccon” in PROJ4 library.

The ATPOL coordinates can be achieved with with the following parameters:

+proj=ccon +lat_1=52 +lon_0=19 +axis=esu +a=6390000 +x_0=330000 +y_0=-350000

Newer version of GIS software, linked with updated PROJ4 library, will allow to use directly ATPOL coordinates in GIS projects.

There is apparently no simple solution to set centrographic tangent conic projection in GIS software built with earlier versions of the PROJ4 library.

The most similar solution could be set with the following custom projection:

+proj=eqdc +lat_1=52 +lat_2=52 +lat_0=52 +lon_0=19 +axis=esu +a=6390000
+b=6390000 +ellps=sphere +x_0=330000 +y_0=-350000

or, when “+axis=esu” is not supported:

+proj=eqdc +lat_1=52 +lat_2=52 +lat_0=52 +lon_0=19 +a=6390000
+b=6390000 +ellps=sphere +x_0=330000 +y_0=350000

The second case will give reversed \(y\) coordinates, counting from lower left (SW) corner.

However, this is only an approximation and results in \(\approx\) 400 m error on the grid edges.

PolBiG in GIS software

According to the original article, the following projection can be set to achieve PolBiG coordinates in GIS software:

 +proj=laea +lat_1=52 +lat_2=52 +lat_0=52 +lon_0=19 +R=6371000 +x_0=512000 +y_0=512000

Implementation strategy

The code is under reorganization! The description below refers to first version of decimal ATPOL without any atypical resolutions (Download section). Since April 2019, the SVN tree is under heavy development to implement atypical resolutions and PolBiG grid. The documentation will be updated after ending of this work!

VBA implementation (for Excel and OpenOffice) is available for download. Other languages passed the tests and the snippets can be browsed in SVN tree.

For each language, two tests for accuracy check are designed and available:

  1. The short test, which computes the points given as a reference below and compares with the reference values. The sum of errors is returned, it should not exceed 1e-10.
  2. The long test, which generates pseudorandom (repeatable) 10 000 pairs of “xy” points and converts each point to latitudes and longitudes. For each grid length in range 2,4,…,10,12 each point is converted to grid and back to coordinates 10 times. Maximal error is reported (it should be around 1e-15). This test is extensive and allowed to catch several floating point rounding errors and deal with them. Beware that the computation is very long, the spreadsheet can hang so do not run this function before backup or besides any production data.

C

Void functions, which require to pass pointers to target variables to store the results. The grid char pointer must point to an allocated place to store grid results there.

void atpol_latlon_to_xy(double lat, double lon, double *x, double *y);
void atpol_xy_to_latlon(double x, double y, double *lat, double *lon);
void atpol_xy_to_grid(double x, double y, char *grid, int len, double *xoffset, double *yoffset);
void atpol_grid_to_xy(const char *grid, double xoffset, double yoffset, double *x, double *y);
void atpol_grid_to_latlon(const char *grid, double xoffset, double yoffset, double *lat, double *lon);
void atpol_latlon_to_grid(double lat, double lon, char *grid, int length, double *xoffset, double *yoffset);

Java

This implementation tries to avoid OOP as much as possible to force consistency with other languages. Methods are static and return object arrays, containing the results.

public static Object[]
    latlon_to_xy(double lat, double lon) // 0 - x (double), 1 - y (double)
public static Object[]
    xy_to_latlon(double x, double y) // 0 - lat (double), 1 - lon (double)
public static Object[]
    xy_to_grid(double x, double y, int len) // 0 - grid (string), 1 - xoffset (double), 2 - yoffset (double)
public static Object[]
    grid_to_xy(String grid, double xoffset, double yoffset) // 0 - x (double), 1 - y (double)
public static Object[]
    latlon_to_grid(double lat, double lon, int len) // 0 - grid (string), 1 - xoffset (double), 2 - yoffset (double)
public static Object[]
    grid_to_latlon(String grid, double xoffset, double yoffset) // 0 - lat (double), 1 - lon (double)

JavaScript

var atpol = {
    latlon_to_xy: function (lat, lon) // returns [x,y]
    xy_to_latlon: function (x, y) // returns [lat,lon]
    xy_to_grid: function (x, y, len) // returns [grid, xoffset, yoffset]
    grid_to_xy: function (grid, xoffset, yoffset) // returns [x,y]
    grid_to_latlon: function (grid, xoffset, yoffset) // returns [lat,lon]
    latlon_to_grid: function (lat, lon, length) // returns [grid, xoffset, yoffset]
}

PHP

class atpol {
    function latlon_to_xy($lat, $lon) // returns array($x, $y)
    function xy_to_latlon($x, $y) // returns array($lat, $lon);
    function xy_to_grid($x, $y, $len=8) // returns array($grid, $xoffset, $yoffset);
    function grid_to_xy($grid, $xoffset, $yoffset) // returns array($x, $y)
    function grid_to_latlon($grid, $xoffset, $yoffset) // returns array($lat, $lon);
    function latlon_to_grid($lat, $lon, $length) // returns array($grid, $xoffset, $yoffset);
}

Pascal

(tested with freepascal compiler)

unit atpol;
interface
procedure atpol_latlon_to_xy(lat : double; lon: double; var x : double; var y : double);
procedure atpol_xy_to_latlon(x: double; y: double; var lat: double; var lon: double);
procedure atpol_xy_to_grid(x : double; y: double; length : integer; var grid: string;
                           var xoffset: double; var yoffset: double);
procedure atpol_grid_to_xy(grid : string; xoffset : double; yoffset : double;
                           var x : double; var y : double);
procedure atpol_latlon_to_grid(lat : double; lon : double; var grid : string;
                               length : integer; var xoffset : double; var yoffset : double);
procedure atpol_grid_to_latlon(grid : string; xoffset : double; yoffset : double;
                               var lat : double; var lon : double);

Perl

latlon_to_xy($lat, $lon) # return($xx,$yy);
xy_to_latlon($x, $y) # return($lat,$lon);
xy_to_grid($x,$y,$len) # return($grid, $xoffset, $yoffset);
grid_to_xy($grid, $xoffset, $yoffset) # return($x,$y);
latlon_to_grid($lat, $lon, $len) # return($lat,$lon);
grid_to_latlon($grid, $xoffset, $yoffset) # return($lat,$lon);

Python

def latlon_to_xy(lat, lon) # return (x, y)
def xy_to_latlon(x, y) # return (lat, lon)
def xy_to_grid(x, y, len=8) # return (grid, xoffset, yoffset)
def grid_to_xy(grid, xoffset, yoffset) # return (x, y)
def grid_to_latlon(grid, xoffset, yoffset) # return (lat, lon)
def latlon_to_grid(lat, lon, length) # return (grid, xoffset, yoffset)

VBA

VBA implementation allows to perform the coordinate conversions inside the spreadsheets:

  1. ATPOL_GRID_TO_LATLON(grid, xoffset, yoffset)
    -returns an array (lat, lon). The offset parameters are optional, default values are 0.5 (the middle of the square).
  2. ATPOL_GRID_TO_XY(grid, xoffset, yoffset)
    -returns an array (x, y). The offset parameters are optional, default values are 0.5 (the middle of the square).
  3. ATPOL_LATLON_TO_GRID(lat, lon, length)
    -returns an array (grid, xoffset, yoffset, x, y). The length parameter is optional (default = 8, i.e. 100 meters square).
  4. ATPOL_LATLON_TO_XY(lat, lon)
    -returns an array (x, y).
  5. ATPOL_XY_TO_GRID(x, y, length)
    -returns an array (grid, xoffset, yoffset, x, y). The length parameter is optional (default = 8, i.e. 100 meters square).
  6. ATPOL_XY_TO_LATLON(x, y)
    -returns an array (lat, lon)
  7. ATPOL_TEST()
    -runs the short test, returns sum of errors
  8. ATPOL_TEST_LONG()
    -runs the long test, returns maximal error (can hang the spreadsheet program, do not run before data backup).

Computational details

The algorithm for ATPOL “latlon” pair to “xy” pair conversion:

  1. \(\lambda = \lambda - \lambda_0\)
  2. \(r = \frac{\cos \varphi_0}{\sin \varphi_0} - \tan (\varphi - \varphi_0)\)
  3. \(x = r \sin (\lambda \sin\varphi_0)\)
  4. \(y = r \cos (\lambda \sin\varphi_0)\)
  5. \(y = y - \frac{\cos \varphi_0}{\sin \varphi_0}\)
  6. \(x = Rx + x_0\)
  7. \(y = Ry + y_0\)

The algorithm for “xy” pair to “latlon” pair conversion:

  1. \(x = \frac{x - x_0}{R}\)
  2. \(y = \frac{y - y_0}{R}\)
  3. \(y = y + \frac{\cos \varphi_0}{\sin \varphi_0}\)
  4. \(\lambda = \frac{\arctan(x/y)}{\sin \varphi_0}\)
  5. \(r = \sqrt{x^2+y^2}\)
  6. \(\varphi = \varphi_0 - \arctan\left(r-\frac{\cos \varphi_0}{\sin \varphi_0}\right)\)
  7. \(\lambda = \lambda + \lambda_0\)

ATPOL Reference values

These reference values (beware of exponents after “b” letter) were computed up to 90 significant digits using Maxima Computer Algebra System. They were also checked in R using MPFR multiple precision library interface.

  lat = 55, lon = 24
  x = 6.500315410 9413219363 4638921909
       2919102347 6549426346 4294406114
       1134263122 2586709523 6877638936 b2
  y = 4.106161777 0643609028 0069398239
       9868109797 7416098516 8475411589
       7741848959 9526507236 9127814945 b0

  lat = 49, lon = 15
  x = 3.707418900 7307473069 6146050746
       2762635775 1822453853 9452623925
       1805565421 1002353757 3371334723 b1
  y = 6.768262355 9270039774 4316813206
       3136538237 1028407494 1210768315
       2116602614 4742493968 5399610358 b2

  lat = 49, lon = 24       
  x = 6.960533606 1617843913 9749832254
       1755018117 4703675369 6342716067
       6503001532 8499992312 2712744907 b2
  y = 6.722945679 5827199940 2311874332
       7574763977 2116443227 5129393298
       2056341816 4582670512 9387468615 b2

  lat = 52, lon = 19       
  x = 330
  y = 350

  x = 0, y = 0
  lat = 5.503040399 3648806391 6131639786
         9569363580 3219644367 1837742899
         2831279682 1573747622 5554628753 b1
  lon = 1.384022731 8521004431 6191689836
         7708417395 0606591263 3069285468
         7864255005 5905203650 9154275744 b1

  x = 700, y = 0
  lat = 5.500351550 5218481835 1436251940
         2356517141 5525549010 2366181839
         2910549810 8234368660 1539449084 b1
  lon = 2.478270718 4271129766 1229102707
         7864236604 5958438506 2611201880
         3643885511 3577052279 0628302380 b1

  x = 0, y = 700
  lat = 4.877384783 4747808675 2723438685
         7484285450 8438794922 2721477719
         9175666700 1434651537 3381662738 b1
  lon = 1.451445359 4615022781 0015146712
         5841166221 7940635007 0428788960
         0558335581 1832098353 1992814714 b1

  x = 700, y = 700
  lat = 4.875047607 0495021286 9950531623
         1417070334 8694846514 1777654287
         4672439505 7853796537 0474833601 b1
  lon = 2.402761076 3560529927 7468614203
         6788418600 5147161668 5964092529
         8571408752 0740760263 6494787753 b1

PolBiG Reference values

  lat = 56, lon = 13
  x = 1.392019982 3328386707 0710502049
       8839469242 9745074455 0002966054
       7518169546 3644069731 5107122351 b2
  y = 9.722952309 6817712493 7531233933
       8243678404 7280049662 0210092747
       6092514781 2404100534 5304762027 b2

  lat = 48, lon = 13
  x = 6.586821311 7074637144 0003501026
       1776786365 8445290974 5902493657
       7595062448 8048752772 2679414374 b1   
  y = 8.548350906 9197720177 4593546938
       7509237139 6431972146 0118376946
       3381801763 1792280625 8877460046 b1

  lat = 48, lon = 25
  x = 9.581317868 8292536285 5999649897
       3822321363 4155470902 5409750634
       2240493755 1195124722 7732058563 b2   
  y = 8.548350906 9197720177 4593546938
       7509237139 6431972146 0118376946
       3381801763 1792280625 8877460046 b1

  lat = 56, lon = 26
  x = 9.467178822 6709726719 6646249220
       8439370352 2615260131 8287358637
       2471574069 7437023660 5156161151 b2
  y = 9.779273085 7417229125 7862733056
       4811346561 3271779203 8208543498
       0996318526 3289486670 3892102446 b2

  lat = 52, lon = 19
  x = 512
  y = 512

  x = 0, y = 0
  lat = 4.718266859 9476215028 0683495067
         5838684537 3721626684 5601807749
         3857259886 0257573143 7436009054 b1
  lon = 1.222042020 8415217468 4738028380
         1168494066 8375424704 4109783093
         2543458421 7889972751 2221761488 b1

  x = 0, y = 1024
  lat = 5.633765916 0299358671 4901337923
         3411240987 1181158115 4086959988
         3837299993 8089182744 9414233005 b1
  lon = 1.067722585 2957877342 3325682050
         7958712032 3166448555 7481147660
         7590757781 8240777654 7885281270 b1

  x = 1024, y = 0
  lat = 4.718266859 9476215028 0683495067
         5838684537 3721626684 5601807749
         3857259886 0257573143 7436009054 b1
  lon = 2.577957979 1584782531 5261971619
         8831505933 1624575295 5890216906
         7456541578 2110027248 7778238512 b1

  x = 1024, y = 1024
  lat = 5.633765916 0299358671 4901337923
         3411240987 1181158115 4086959988
         3837299993 8089182744 9414233005 b1      
  lon = 2.732277414 7042122657 6674317949
         2041287967 6833551444 2518852339
         2409242218 1759222345 2114718730 b1

  x = 512, y = 512
  lat = 52
  lon = 19

OpenATPOL is created and maintaned by Lukasz Komsta.

This site uses my own retro design inspired by an old Cecil spectrophotometer.

Released under GPLv3 license. Last update: 2019.04.30